Geçmişten günümüze kadar gelen çağlara göre matematiğin kronolojik sıralaması Matematiğin varoluşundan bu yana kadar gelen tarihi gelişimini sizlere aktarıyoruz.

Geçmişten günümüze kadar gelen çağlara göre matematiğin kronolojik sıralaması
Matematiğin varoluşundan bu yana tarihsel gelişimini sizlerle paylaşacağız. Matematikçiler Birinci ve İkinci Grup olarak 2 gruba ayrılır. Bunlar milattan önce yaşamış olan matematikçiler ve milattan sonra yaşamış olan matematikçilerdir.
Antik Çağ’da ilk önemli matematik merkezi MÖ 2000’lerden sonra Babilliler olmuştur. Ekonomik yapılarının gerektirdiği denklem çözme, kök bulma, alan ve hacim hesaplama gibi tekniklerin yanı sıra astronomiye duydukları yakın ilgi nedeniyle trigonometriyi geliştirmişlerdir. En kayda değer katkıları, sıfır sembolünün eklenmesiyle ondalık sisteme çok benzeyen 60 taban sayı sistemiydi. Bu sistem bugün hala açı ve zaman ölçümlerinde kullanılmaktadır.
Eski Mısır’da Golenişev papirüsü (M.Ö. 1900 civarı) ve Rhind papirüsü (M.Ö. 1700’den önce) olarak adlandırılan matematiksel metinler, erken aritmetik ders kitapları olarak nitelendirilebilecek, dönemlerinin önemli eserleriydi. Matematik bu kültürlerde pratik bir araç olmanın ötesine geçemeyecektir. Yunan matematiği M.Ö. 600 yıllarında komşu Mezopotamya ve Mısır’dan bilgi toplayarak ortaya çıkmıştır. Yaklaşık M.Ö. 5. yüzyılda kendi eserlerini üretmeye başlamıştır.
Elealı Zenon, Antik Yunan’da matematik, tarih, kronoloji ve fizik gibi kavramlar üzerine araştırmalar yapan bir okulun lideriydi. Birçok deney yaptı ve zaman ve uzayın sonsuz sayıda parçaya bölünmesiyle ilgili paradokslar yarattı ve Demokritos’un atomistik görüşleri geometrik büyüklüklerin ölçümü için yeni aksiyomlar gerektirdi ve teorik matematik kavramını oluşturdu. MÖ 4. yüzyıl matematikçileri, rasyonel sayıların (tam sayıların birbirlerine oranları) niceliklerin ölçümü için yeterli olmadığını görmüş ve irrasyonel sayıların geometrik teorisini geliştirmişlerdir. Alan ve hacim hesaplamalarında sonsuz küçük kesitler bugünkü integral kavramının ilk işaretleri olarak görülebilir.
Teorik matematiğin sonsuzluk fikrinin dışında, Antik Yunan matematiğinin en önemli iki konusu astronomiden kaynaklanan konikler ve küresel geometri problemleriydi. MÖ 4. yüzyılın sonunda yapılan çalışmalar, daha sonra yazılan Eukleides’in ünlü Stoikheia’sı (Elementler) ile sembolize edilir.
Teorik matematik antik çağda Arşimet ve Apollonius ile zirveye ulaşmıştır. Koniklerle ilgili bulguların önemi ancak 19. yüzyılda projektif geometrinin gelişmesiyle anlaşılmıştır. Arşimet ve Apollonius’tan sonra ilerleme astronomiden kaynaklanan problemler tarafından yönlendirilmiştir. Gezegenlerin yörüngelerinin belirlenmesi, sayısal tablolar ve diğer keşifler MS 2. yüzyılda Batlamyus’un astronomi alanındaki bulgularına yol açmıştır. MS 4. yüzyıldan sonra bilim, eski bulguların gözden geçirilmesi ve öğretilmesine dönüştü. Klasikler yeniden yorumlandı ve eski kitaplar üzerine yeni tezler yazıldı. Zaman geçtikçe Bizans döneminde Yunan matematiğinin sadece basit bir özeti kaldı.
Orta Çağ’da bilim Hindistan’da ve İslam dünyasında yeniden canlandı. Bağdat’ta, Abbasi halifesi Mansur’un etkisiyle, Yunan bilimsel eserlerinin sistematik bir çevirisi yapıldı. Hint astronomisinin etkisiyle Bağdat, matematik ve astronomi için önemli bir merkez haline geldi. Matematik ve astronominin bu canlanmasındaki önemli faktörlerden biri Harezmi’dir (yaklaşık 780 – yaklaşık 850). Harezmi Bağdat okulundandı ve özellikle trigonometri ve küresel trigonometri alanlarında antik dönemin çok ötesinde bir gelişmeye öncülük etti. İslam matematik ve astronomi geleneği 1400’lü yıllara kadar kesintisiz devam etmiştir.
İslam biliminin Avrupa’ya yayılması 11. yüzyılda başlamıştır. Bu konudaki öncüler 11. yüzyılda İngiliz filozof Bathlı Adelard ve 12. yüzyılda İtalyan matematikçi Leonardo Pisano’dur. Bu yüzyıllarda Yunan bilim klasikleri Arapça’dan Latince’ye çevrilmiş ve bugün Rönesans olarak adlandırdığımız dönemin temelini oluşturmuştur.
16. yüzyılın ortalarında Kopernik’in astronomi ve Vesalius’un anatomi alanındaki keşifleri eski klasiklerin hatalarını ortaya çıkarmıştır. İtalya’da del Ferro Cardano Tartaglia ve Ferrari’nin üçüncü ve dördüncü derece denklemlere buldukları çözümler matematikte yeni bir çağın habercisi olan ilk keşiflerden bazılarıydı. Viete bilinmeyen nicelikler için harfler kullanacak ve bu da daha sonra sembolik cebirin yolunu açacaktır.
17. yüzyılda Napier logaritmayı icat etmiştir. Cavalieri, Kepler’in sonsuz küçükler için geliştirdiği yöntemleri geometriye uyguladı. Örneğin, bir elipsin alanı bu yöntemle hesaplanabiliyordu. 1637’de Descartes büyük keşfi olan analitik geometriyi yaptı. Fermat’nın katkılarıyla analitik geometri, geometri problemlerini cebirsel problemlere dönüştüren yeni bir araç haline geldi. Fermat matematiği bir yan uğraş olarak sürdürmeye devam etti ve sayılar teorisi ve olasılık teorisindeki keşifleri ona en büyük amatör matematikçi unvanını kazandırdı.
Newton’un Philosophiae naturalis principia mathematica (1687; Doğa Felsefesinin Matematiksel İlkeleri) adlı eseri bugüne kadar yazılmış en büyük bilimsel çalışma olarak kabul edilir. George Boole, Leibniz’in evrensel nitelikler için geliştirmeyi amaçladığı sembolik mantığı ancak 19. yüzyılın ortalarında tanıtmıştır. Newton ve Leibniz’in 17. yüzyılın ikinci yarısında diferansiyel ve integral hesabı keşfetmeleri matematikte çok önemli bir adıma işaret eder. Newton’un temel amacı doğayı anlamaktı; Leibniz ise bilgiye giden yolu açmak istiyordu.
18’inci yüzyıl matematiğinin en önemli ismi Leonhard Euler’dir. Bu matematikçi, analiz ve sayılar teorisi başta olmak üzere matematiğin hemen her dalına önemli katkılarda bulunmuştur. Diğer büyük 18. yüzyıl matematikçileri arasında J.-L. Lagrange, J. L. R. d’Alembert ve P.-S. Laplace ve G. Monge sayılabilir.
19. yüzyılda önemli bir gelişme de Öklidyen olmayan geometrilerin ortaya çıkmasıydı. Eukleides geometrisi Stoikheia’da ortaya konan beş Aksiyoma dayanıyordu. Yüzyıllar boyunca matematikçiler, “bir noktadan verilen bir doğruya yalnızca bir paralel çizilebileceğini” belirten beşinci Aksiyomu kanıtlamaya çalışmışlardır. 1854 yılında iki matematikçi (Rusya’da N. I. Lobachevsky ve Macaristan’da J. Bolyai) ve Alman matematikçi B. Riemann, paralellik aksiyomu olmaksızın da tutarlı geometrik modeller inşa edilebileceğini bağımsız olarak gösterdiler. Felsefi öneminin yanı sıra Riemann’ın bulguları daha sonra Einstein’ın görelilik kuramının matematiksel temelini oluşturacaktır. 19. yüzyılın en büyük matematikçilerinden biri olan C. F. Gauss, matematiğin hemen her dalına önemli katkılarda bulunmuştur.
19. yüzyıl sadece hızlı bir gelişmeye değil, aynı zamanda matematiğin aksiyomatik yapısının sorgulanmaya başlandığı bir dönem olmuştur. Weierstrass ve Dedekind’in gerçek sayılar üzerine bulguları ve Cantor’un sonsuz küçükler sınıflandırması aksiyomatik yapıya ışık tutmuştur.
Matematiğin gelişiminde birkaç problemin özel bir yeri olmuştur. Fermat’ın çözdüğü ve bir kitabın kenarına yazdığı ünlü problem (x” denklemini sağlayan x y z tam sayıları yoktur) n = 3 4 … için + y” = z”) Fermat problemi olarak bilinir {bkz. Fermat’ın büyük teoremi). Ancak 300 yıldır hiç kimse Fermat problemini çözemedi. Problemi çözme çabaları matematiğe çok şey kazandırmıştır.
Birinci Grup Matematikçiler
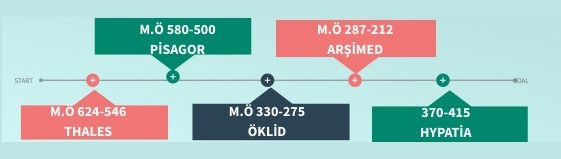
- Thales (M.Ö. 624-547)
- Pisagor (M.Ö. 569-500)
- Zeno (M.Ö. 495-435)
- Eudexus(M.Ö. 408-355)
- Öklid (M.Ö. 330-275)
- Arşimed (M.Ö. 287-212)
- Apollonius (M.Ö. 260-200)
- Hipparc-hos (M.Ö. 160-125)
- Menaleas (doğumu
 M.Ö. 80)
M.Ö. 80) - İskenderiyeli Heron (? -M.S.80)
- Batlamyos (85- 165) ve Diophantos (325-400)
M.Ö. 8. yüzyıl ile M.S. 2. yüzyıl arasında ikinci grup olarak belirttiğimiz Batı Dünyası matematikçileri ise 16. ile 20. yüzyıl arasında yaşamışlardır:
İkinci Grup Matematikçiler;
- Johann Müler (1436-1476)
- Cardano (1501-1596)
- Descartes (1596. 1650)
- Fermat (1601-1665)
- Pascal (1623-1662)
- Newton (1642-1727)
- Leibniz (1646-1716)
- Leibniz (1646-1716)
- Mac Loren (1698-1748)
- Bernoulliler (Bu aileden sekiz ünlü matematikçi vardır. Bunlar; Jean Ber-noulli l667-1748 Jacques Bernoulli 1654-1705 Daniel Bernoulli 1700-1782…)
- Euler (1707-1783)
- Gespard Monge (1746-1818)
- Lagrance (1776-1813)
- Joseph Fou-rier (1768-1830)
- Poncolet (1788-1867)
- Gauss (1777-1855)
- Cauchy (1789-1857)
- Lobaçevski(1793-1856)
- Abel (1802-1829)
- BooIe (1815-1864)
- Riemann (1826-1866)
- Dedekind (1831-1916)
- H. Poincare (1854-1912)
- Cantor (1845-1918)
Matematik tarihi kronolojisi sayfasında bu bilime katkıda bulunan bilim adamları hakkında bilgi verilmiştir.
İlgili Yazılar:
Belirli açıların trigonometrik değerleri
 M.Ö. 80)
M.Ö. 80)